前言
在现实生活中,我们常会遇到需要判断某元素是否在一个集合中的问题。比如,网络爬虫需要判断一个网址是否已经被爬取过、或者需要检查某个邮件地址是否用于发送垃圾邮件。
我们可以想到的方法可能是把他们保存起来,保存到数组、链表、树中,并由最优的搜索算法遍历。但随着数据个数的增长,搜索的代价逐渐升高(最好的情况是O(logn)),且空间占用会扩大。这时,我们想到哈希函数,通过把数据映射到哈希值,搜索速度提升(O(n/k)),而且数据可以得到压缩。那么,我们要问,如果数据个数再增长呢?哈希值存不下呢?这时,为了保证可用性,我们不得不牺牲掉一些准确性,这就是布隆过滤器的思想。
布隆过滤器
原理介绍
布隆过滤器由布隆在1970年提出,它由一个很长的二进制数组和一系列哈希函数组成。通过在数组上记录每个元素的指纹,来记录需要过滤的元素的信息。
假设现在有3个元素需要加入过滤器,同时有3个哈希函数。我们先将过滤器初始化,即全部置0。然后对每个元素通过每个哈希函数求哈希值,并将这9个哈希值对应的数组上的点置1。全部操作完成后,布隆过滤器就完成了。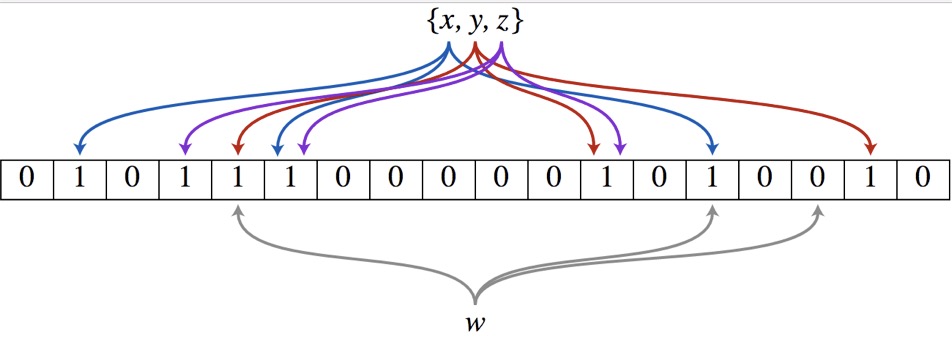
在实际使用中,用哈希函数对需要判断的元素求哈希值,如果所求得的哈希值在数组对应位置上出现0,则可以确定该元素一定不是需要过滤的元素。但是,如果发现哈希值对应到数组上都为1,那么,该元素有一定概率是不需要被过滤的,这也是导致布隆过滤器误删的原因。
误差计算
我们现在来计算一下布隆过滤器误删元素的概率。假设数组长度为m,哈希函数个数为h,需要过滤的元素个数为k。
我们先在过滤器中插入元素。一个元素在一个哈希函数作用下,造成数组中某位被置为1的概率为$ 1 \over m $,因而该位没有被置1的概率为:$$ 1 - {1 \over m} $$
则一个元素在所有哈希函数作用后,该位仍为0的概率为:$$ (1-{1 \over m })^h $$
接下来,把所有需要过滤的元素插入过滤器后,该位为0的概率变为:$$ (1-{1 \over m })^{hk} $$
因而在布隆过滤器完成时,某位被置为1的概率为:$$ 1-(1-{1 \over m })^{hk} $$
现在我们使用完成的布隆过滤器过滤元素。对于被检验的某个元素,得到它的哈希值对应数组位置都被置1的概率为:$$ [1-(1-{1 \over m })^{hk}]^k $$
即该元素被删掉的概率。
我们知道,在m很大时,$ (1-{1 \over m })^{hk} \approx e^{-hk / m} $,则原概率约等于:$$ (1-e^{-hk/m})^k $$
我们可以发现,被误删的概率随着数组长度(m)的增大而减小,随着需要过滤元素个数(k)的增大而增大。

